The International Tinnitus Journal
Official Journal of the Neurootological and Equilibriometric Society
Official Journal of the Brazil Federal District Otorhinolaryngologist Society
ISSN: 0946-5448

Google scholar citation report
Citations : 12717
The International Tinnitus Journal received 12717 citations as per google scholar report
The International Tinnitus Journal peer review process verified at publons
Indexed In
- Excerpta Medica
- Scimago
- SCOPUS
- Publons
- EMBASE
- Google Scholar
- Euro Pub
- CAS Source Index (CASSI)
- Index Medicus
- Medline
- PubMed
- UGC
- EBSCO
Volume 26, Issue 1 / June 2022
Original Paper Pages:42-49
10.5935/0946-5448.20220006
A Resonant Circuit Involving the Vestibule and Cochlea Base Could Cause Extremely Low-Frequency Tinnitus, also called "The Hum" or "Taos Hum"
Authors: Franz Gunter Frosch
PDF
Abstract
Introduction: “The Hum” or “Taos Hum” are common names for the sound associated with tinnitus at extremely low frequencies.
Objectives: This study aimed to identify the cause and place of origin of the hum using relevant data from the literature along with data extracted from a questionnaire and other related information.
Results and Conclusion: The vestibule and cochlea base seem to play a crucial role in the generation and elimination of the hum. The origin of the hum seems to appear in a region near the vestibule and cochlea base, in which a phase resonance could occur between the electrical signal of the vestibule, the sound pressure signal of the cochlear base, and External Sounds.
Introduction
A rare extreme low-frequency tinnitus, called hum, has been found to be perceived like an External Sound (ES) or a mixture of ESs at extremely low frequencies ranging from 30 Hz to 80 Hz, sometimes at fluctuating volumes. Furthermore, the kinds of subjective hearing have been found to greatly vary among hum-affected subjects. Characteristically, people affected by hum often claim it originates from an external source. Therefore, the hum is often named after the locations from which increased nuisance from an alleged low-frequency noise is reported, e.g., “Taos Hum” [1].
Hum reportedly not only interacts with ESs as beats and/ or by getting masked, but it also may get influenced by rotational forces, changes in body position, and moving long distances, such as with air travel [2-5].
It is important to know how and where beats are processed in the ears since beat-interactions between an ES and hum are used to determine the frequency and loudness of the hum [3].
The term ‘Acoustic Beat’ (AB) has been classically used to describe the interference between two ESs of slightly different frequencies, perceived as periodic variations in their volumes at a rate corresponding to the difference between the two frequencies. Our knowledge of the phenomenon of ABs has grown significantly in the field of musical harmony. ABs were already known to early musicians [6].
Synchronous ABs are considered to be at the same Beat Frequency (BF). When two simultaneously presented ABs are synchronous, they are called Double Beats (DBs), and their phase relations are constant and can be determined. They are in-phase when the ABs have the same rhythm and anti-phase when they sound in the opposite direction. Phase relations in between are also possible. In-phase DBs can be psychoacoustically differentiated from anti-phase DBs. Therefore, if the AB relationship of two synchronous in-phase ABs is inverted abruptly by 180°, a psychoacoustic change in the phase relationship can be easily perceived. The abrupt change is impressively audible when very low BFs below 0.05 Hz are used at volumes where the low volume period of the AB is not audible. A 180° phase change of one of the ABs changes an audible AB into a non-audible AB and vice versa. In addition to a short click as an indicator of the phase switch and volume change of the AB, no other changes can be observed. As two ESs of approximately similar frequencies have been found to not increase or decrease in loudness when the phase of one ES is reversed, it appears that the basilar membrane is not sharply tuned but a critically damped element. If sharply tuned, there should have been a temporary increase in loudness in the non-inversed ES [7].
The auditory system uses frequency-limited critical bands to process its input in the frequency domain. Two simultaneously presented neighboring ESs can be heard as beating sounds and can only be heard separately if they are located in different critical bands. Two invariant filter attributes, a logarithmic relationship between the filter bandwidth and center frequency and a level-independent bandwidth, are essential. As the filter bandwidths of the cochlea and peripheral neurons are level-dependent and vary over a wide range, the required invariances of the critical band filter are assumed to be derived more centrally through processing mechanisms. The laminar organization of collicular neurons may be essential for the generation of critical bands and the perception of periodicity pitch and sound localization. The mechanisms underlying the generation of the corresponding physiological bandpass filters are unknown [8].
Outer Hair Cells (OHCs) exhibit several properties. Thus, Cochlear Microphonic Potentials (CMs) are generated at the apical ends of OHCs and follow the waveform of acoustic input [9]. Phases between the stapes and microphone are strongly frequency-dependent and seem to be the main source of group delay. The phase is approximately flat between the stapes and CMs from the round window, indicating negligible group delay. Although a significant group delay has been observed at low frequencies, the delay did not change at different frequencies, which is inconsistent with the frequencydependent phase delay of the cochlear traveling wave. The group delay of the microphonic potential recorded at the round window may not reflect the propagation delay of traveling waves within the cochlea under physiological conditions [10].
A major problem is how pitch is extracted from acoustic waveforms and represented in the auditory system. Place and timing theories have been debated for over a century but remain controversial [11].
The essential functions of the inner ear, previously attributed to traveling wave-induced Basilar Membrane (BM) mechanics, are increasingly being challenged. Two mutually exclusive schools of thought for cochlear tuning along the BM, OHCs, Inner Hair Cells (IHCs), and Auditory Nerve Fibers (ANFs) are competing. The traditional “BM-first” hypothesis follows Bekesy and states that the acoustic activation sequence at the hearing threshold in the inner ear is BM-OHC-BM-IHC-ANF. Second, the “OHC-First” hypothesis assumes that it is OHC-IHCANF, with the concurrent OHC-BM branch being an epiphenomenon. Only the “OHC-First” hypothesis of cochlear activation is compatible with the findings of a meta-analysis. The results indicated that dual tuning, when the BM and organ of Corti are tuned separately, is consistent with the concept of overload protection of the organ of Corti sensitivity as the genuine function of BM tuning [12].
Most scholars still consider the inner ear functions of the vestibular system, which is responsible for equilibrium only, to be separate from the cochlea, which is responsible for hearing.
However, Vestibular Hair Cells (VHCs) are sensitive to body movements and ESs. Acoustically responsive irregularly discharging vestibular afferents innervate the saccule and are presumed to activate reflexes on the neck muscles (sternocleidomastoid), periocular, and middle ear muscles [13].
The extensive mutual influence between the cochlea and the three semicircular canals was described as early as 1953. The sound-induced pressure change of the cochlear fluids close to the oval window is in-phase with the velocity of the displacement of the cupula, stapes, and BM. Because displacement of the BM is accompanied by a gliding motion of the tectorial membrane relative to the organ of Corti, the microphonics are in-phase with the displacement of the tectorial membrane (of the base). This appears to be a general relationship for all labyrinth organs [14].
Here, we will examine the reported features of hum and ascertain whether comparable phenomena are described in the literature to gain better insight into the conceivable location and possible causes or circumstances for the formation of hum. The features of hum were assessed using data extracted from a questionnaire [2], previous case studies [3-5], data sourced from the literature and additional measurements. The probable origin and action areas of hum are discussed. Moreover, as many hum sufferers have reported that their hum disappears during head movements, we also included the vestibular system in our study.
Methods
The principles of the methods used have already been reported in a previous study [3] in the chapters “Investigations on Hum,” “Sound Generation,” and “Sound Interactions.” The unreported parts of the methods used are described below.
Interactive hum has been reported to interact with ESs to form beats, have a time lag of two to three days until it reappears after long distance air travel, and stops during horizontal head rotation. The rare simultaneous occurrence of all three phenomena has been found to be present in only 7% of hum-affected people [4]. All other humaffected people tend to present typical characteristics and progression, as described in fora. All supplementary measurements were performed by the author on his own hum.
Stimuli were produced using digital Test Tone Generator (TTG) software on a notebook. Each TTG consists of one left and one right channel to install two separate sound signals in the notebook. The phase of the left channel in the TTG can be shifted relative to the right channel by up to 360°. Several TTGs can be installed simultaneously in notebooks.
Volume Dependence of Variances of BFs in ABs: The best beat of an AB generally consists of two neighboring primary tones of equal volumes. The best beats of our test were generated with one primary of 1024 Hz and one at 1027 Hz, at test volumes of 11, 32, 51, and 71 dB SPL. For each test, 100 consecutive ABs were stopped with a calibrated customary electronic time clock, and calculated according to the usual methods. Ten measures were taken for each of the four test volumes in a randomly alternating sequence, and the obtained variances were statistically tested to determine whether higher beat volumes lead to significantly higher variances using a one-sided F-test and pairwise comparison of the variances of all six combinations of the four tests. An F-value <3.18 indicated no significant difference between the tested pairs of ABs at the 5% level of error.
Perceiving In-Phase DBs: In the DB experiment, we used two TTGs running simultaneously in a notebook. The two primary tones of the first AB signal were each generated in one of the left channels of the two TTGs to achieve a BF of 3.5 Hz at a well-perceptible best beat in the left channel of the notebook, which was connected to channel one of the oscilloscope. The two primary tones of the second beat signal were each generated in one of the right channels of the two TTGs at a well-perceptible best beat, but at a BF of 3.6 Hz in the right channel of the notebook, which was connected to channel two of the oscilloscope.
Channels 1 and 2 of the oscilloscope were merged into the right channel of the headphones to perceive the two single ABs as one DB in the right ear. The run/stop button of the oscilloscope was set to run for several cycles while listening to the evenly shifting phase relation of the two ABs to obtain a clear impression of the perceived beat shifts while the screen was covered and was set to stop by pressing the stop button when the subject perceived an in-phase rhythm of the DB. Ten measurements were made for each setting. Using the cursor of the oscilloscope, the phase difference between the first and second AB (PD1-2) was measured in ms and tested for normal distribution using the Anderson-Darling test. Then, the significance of a deviation from the in-phase situation was assessed using the Student’s t-test to compare the two mean values of the paired samples. Only normally distributed samples were included in the t-tests. A t-value >2.262 indicated a significant phase difference between the two ABs measured on the oscilloscope when perceived as inphase DB at the 5% level of error.
Hearing Thresholds (HTs) before and during the Valsalva Maneuver: The HTs were measured in the usual manner before and during the Valsalva maneuver. The subjects performed the Valsalva maneuver by moderately forceful attempted exhalation against a closed airway by closing their mouth and pinching their nose shut while expelling air as if blowing up a balloon.
Results
Volume Dependence of Variances of BFs in ABs: The best beats of 3 Hz were measured at four different volumes, from small to high volume beat impressions. The results are in Table 1, which shows that ABs at higher volumes do not vary significantly more than those at lower volumes.
| Test | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| volume | 11dB SPL | 32 dB SPL | 51 dB SPL | 71 dB SPL |
| mean | 2.999Hz | 2.997Hz | 2.'997Hz | 2.996Hz |
| std.dev | 0.0032Hz | O.0049Hz | 0.0036Hz | 0.0033Hz |
| measures | 10 | 10 | 10 | 10 |
| No significant differences of pairwise comparions if Fx/y <3.18 | ||||
| Fl/2=0.42 | Fl/3=0.79 | Fl/4=0.93 | ||
| F2/4=2.19 | F2/3=1.86 | F3/4=L18 | ||
Table 1: Volume dependence of variances of BFs in ABs. Four sets of best beats with ABs of 3 Hz were generated by the interaction of two neighboring primary ESs of 1024.0 Hz and 1027.0 Hz at volumes of 11, 32, 51, and 71 dB SPL by each primary pair which ranged from small to high volume beat-impression. The results were statistically tested for equality using the one-sided F-test by pairwise comparisons of the variances obtained
Perceiving In-Phase DBs: At the used difference of 0.1 Hz of the BFs, the two ABs that generated the DB were only almost synchronous, because their phase relation slowly shifted uniformly. The chosen setup allowed an objective, reproducible measurement of different Mean Frequency (MF) combinations. The measured phase difference between the first and second AB (PD1-2) did not differ significantly from being perceived in-phase except for at a MF1 of 68 Hz (Table 2).
| MF2 | dB1 | MF2 | dB2 | PD1-2 | t-value |
|---|---|---|---|---|---|
| 68 | 59 | 177 | 46 | 18 | 1.6 |
| 68 | 54 | 177 | 46 | 123 | 10.1 |
| 68 | 44 | 2177 | 34 | 98 | 12.8 |
| 254 | 29 | 1034 | 35 | -5 | 0.6 |
| 326 | 39 | 2177 | 34 | -1 | 0.1 |
| 1502 | 29 | 4502 | 46 | -1 | 0.1 |
| 1502 | 32 | 6502 | 46 | -9 | 1.1 |
| 3080 | 39 | 2175 | 40 | 4 | 0.4 |
| 3175 | 39 | 4175 | 40 | 4 | 0.5 |
| 3175 | 39 | 6175 | 46 | 7 | 1.8 |
| 3175 | 45 | 4175 | 46 | 2 | 0.3 |
| 3175 | 31 | 4175 | 45 | -1 | 0.1 |
| 3175 | 45 | 7175 | 51 | -8 | 1.0 |
Table 2: Phases of in-phase perceived DBs. Measures were performed in the right ear at the actual hum frequency of 65 Hz. The first AB consisted of two primaries forming MF1 in Hz, of equal volumes (dB1) in dB SPL, with a BF1 of 3.5 Hz. The second AB consisted of two primaries at MF2, equal volumes (dB2) in dB SPL, but with a BF2 of 3.6 Hz. The MF1 of 68 Hz results from primaries of 66.25 Hz and 69.75 Hz. The phase difference between the first and second AB (PD1-2) was measured in ms and tested for significance. A t-value >2.262 indicates a significant phase difference measured between the two in-phase perceived ABs forming the DB.
HTs Before and during the Valsalva maneuver: HTs were measured before and during the Valsalva maneuver in dB SPL at 200 Hz and at the actual hum frequency of 67 Hz. The HTs deteriorated during the maneuver by 14 dB, during which the perception of the hum did not change.
Behavior of Hum during Purposeful Head Movements: About 36% of hum-affected people perceive a motionsensitive hum that stops during purposeful head movements (yes/no= 62/109), which differs from Frosch [5] due to an error in their Table 2.
A supplementary detailed evaluation of the responses to the original questionnaire [2], where it was asked whether the hum changed because of head movements like rotation (1), nodding (2) or posture changes (3) [5] revealed that a motion-sensitive hum was reported to stop in 52%, 8%, and 13% during horizontal head rotation, nodding, and body position changes, respectively, along with several other body changes. These motions all relate to changes in head position that affect the vestibular system.
The mean resting discharge rates of the vestibular neurons are in the frequency range of the hum. Rapid head shaking alternately brings them above and below of this range [15], which may cause the hum oscillation to stop [3].
Such manipulation may be consistent with a reported activation/elimination of tinnitus with certain head movements, which was accompanied by a concomitant 20 dB worsening of the HT after body position changes [16].
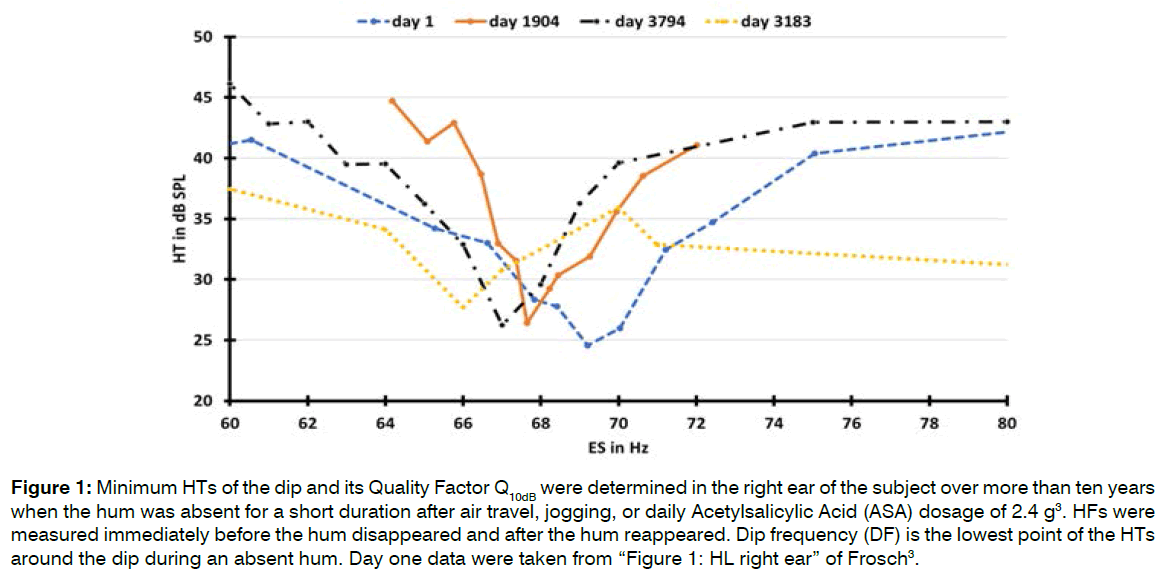
Long Term Behavior of the Dip and Hum Frequency (HF): It is known that hum interacts with ESs, making it challenging to correctly measure HTs and determine a dip in the HT during a present hum. When hum is absent, a dip in the HT at the HF can be easily measured (Figure 1 and Table 3).
Figure 1: Minimum HTs of the dip and its Quality Factor Q10dB were determined in the right ear of the subject over more than ten years when the hum was absent for a short duration after air travel, jogging, or daily Acetylsalicylic Acid (ASA) dosage of 2.4 g3. HFs were measured immediately before the hum disappeared and after the hum reappeared. Dip frequency (DF) is the lowest point of the HTs around the dip during an absent hum. Day one data were taken from “Figure 1: HL right ear” of Frosch [3].
| Day | HFs In Hz | HVs in dB SPL | DFs in Hz | Q10dB | Cause |
|---|---|---|---|---|---|
| 1 | 69 | 40 | 69 | 10 | air trip |
| 1904 | 68 | 40 | 68 | 19 | jogging |
| 3183 | 66 | 37 | 66 | - | ASA |
| 3794 | 67 | 43 | 67 | 16 | air trip |
Table 3: HT measurements at hum frequencies (HFs) and dip frequencies (DFs) and the quality factors Q10dB were graphically determined from the individual curves in Figure 1. HFs and perceived hum volumes were determined according to previously described methods [3] shortly before and after the cause for the hum to disappear. The determination of Q10dB during ASA consumption on day 3183 was not possible because the ambient threshold did not deteriorate by at least 10 dB.
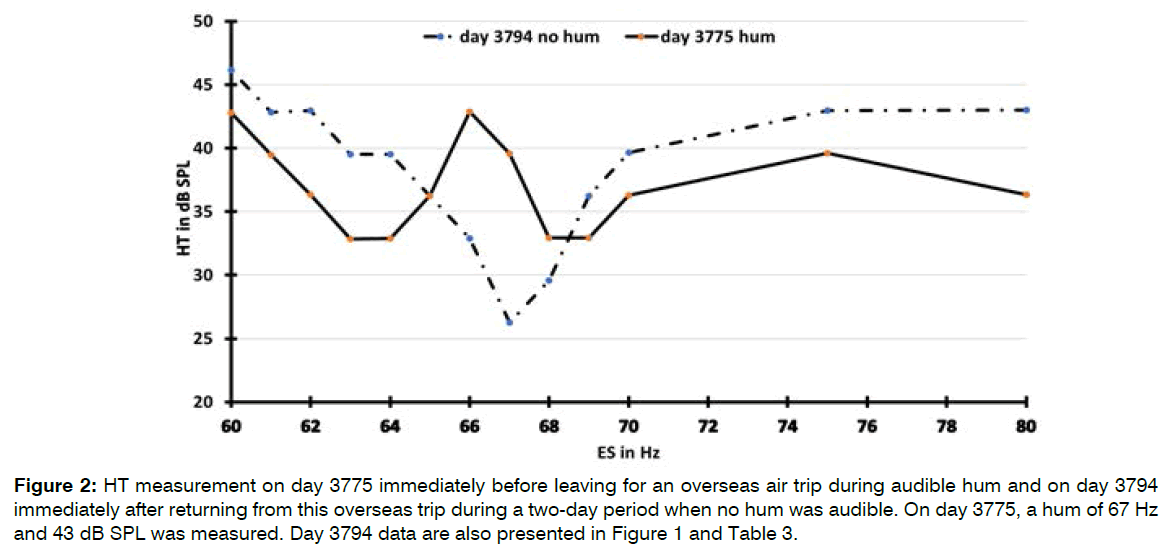
HTs during a Present and Absent Hum: The HTs of an ES around the HF during one consecutive period with and with no hum are presented in Figure 2. The HTs were significantly lower with hum than with no hum when measured approximately 2 Hz above and below the HF, indicating better HTs in the presence of hum. When the hum was inaudible, a slight beat could still be felt at the HT of the ES, indicating that hum oscillation or external noise at a much lower level was still present.
Figure 2: HT measurement on day 3775 immediately before leaving for an overseas air trip during audible hum and on day 3794 immediately after returning from this overseas trip during a two-day period when no hum was audible. On day 3775, a hum of 67 Hz and 43 dB SPL was measured. Day 3794 data are also presented in Figure 1 and Table 3.
Discussion
Speech Analysis in the Ear: Kellaway [7] stated that the BM is not sharply tuned but a critically damped element that remains unnoticed for a long time
It has also been proven that oscillations of the BM induced by the traveling wave run into saturation at medium ES levels above 40 dB SPL, where they can no longer distinguish small frequency differences. Fiber tuning curves near formant peaks broaden, and activity spreads to fibers between the peaks, limiting the dynamic range of all fibers. This is evidence that the neuronal activities at the Characteristic Frequency (CF) do not analyze speech because it is known that speech can be understood without problems even at very high volumes [17].
Volume Dependence of the Variances of BFs in ABs: We assessed whether the ABs were subject to reduced signal accuracies when their volumes increased by statistically comparing the resultant standard deviations of the stopped ABs. The results of all six pairwise comparisons of the four tests in Table 1 have F-values far below the critical table F-value of 3.18, above which it would indicate a significant difference. Therefore identical signal accuracies for all volumes at the 5% level of error are evident, indicating that higher sound volumes of ABs do not influence the accuracy of rhythm detection.
The evidence that the neuronal activities at the CF do not analyze speech must therefore also be applied to ABs because the high accuracy of measured ABs is independent of volume. ABs are not managed at the CF but in a different area
Perceiving In-Phase DBs: The rhythm of two simultaneously presented synchronous best beats of ABs, called Double Beats (DBs) is an instrument for detecting influences on the phase of an AB by creating a reference point for its phase with the second AB of the DB.
Table 2 shows that in-phase perceived DBs were generally measured in-phase at the oscilloscope in parallel to the used headphone over the entire frequency range unless hum was in the interacting area of one of the two ABs. Hum disturbs the in-phase harmony of the perception of DBs, resulting in a phase shift of the AB that is neighboring the hum relative to the second AB.
Hum and one or both of the primaries of an AB affected by hum must have been in the same interaction space; otherwise, the in-phase relationships of the DB would not have been affected.
If we keep in mind the not existing volume dependence of variances of BFs in an AB and the resultant conclusion that ABs are not managed at the CF, it is a logical conclusion that DBs, including their phase relations and interactions with hum, are also not managed at the CF of the primaries in question, but in a different area. This is an area where hum is also active. The ability of an ES to interact with hum, producing beats, periodic pulling and entrainment3 may cause the phase shift of a DB.
The first three rows of results in Table 2 at MF1=68 Hz can be explained by the mutual interference between the current hum of 65 Hz and the one primary tone in the immediate vicinity of the hum, shifting the phase of the primary and thus the entire AB in question. Lower intensities of the primary become stronger influenced by hum, resulting in an increase of the out of in-phase situation of the DB.
It follows that the BM oscillations induced by traveling wave motion cannot be responsible for the measured accurate phase transport required for correct perception of DBs, that the sites of DB generation and hum generation are identical, and that DBs are not processed in the CF but in another area that can rapidly and accurately transmit small signal differences to the brain and in which phase is important.
Hum during Purposeful Head Movements: Hum disappears during purposeful head movements and interacts with ESs [3-5], suggesting that vestibule and cochlea are involved in the generation of hum. Because of the expected strong secondary line-signal mixing and damping of the generated Vestibular Microphonics (VMs) and CMs, the signals are expected to interact only in a spatially limited area encompassing the vestibule and cochlear base, which we refer to as the Vestibule-Cochlea Interaction Area (VCIA).
The origin of hum is most likely in the VCIA, since it can be assumed that the vestibule, as part of the VCIA, is sensitive to head rotation and may generate the in-phase harmony of DBs, since harmony is disturbed by hum.
Since the hum affects the phases of the DBs, it can be concluded that DBs also originate in the VCIA, as do the ABs and speech analysis. Consequently, it can be concluded that the area where ABs and DBs are managed, where speech analysis begins, and where the hum interacts with sounds is the VCIA.
Long term behavior of dip and HF: Figure 1 and Table 3 show that the long term frequency changes of the dip and hum coincide perfectly. The hum of this type depends on the presence of a dip and not vice versa. This conclusion is inferred from the fact that a dip was still present during an absent hum in Figure 1.
This dependence was also observed for the simultaneous presence of Spontaneous Otoacoustic Emissions (SOAEs) and dips. The frequencies of dips coincided almost perfectly with the corresponding SOAEs. SOAEs without exception are located in dips. However, dips do not necessarily contain SOAEs. Therefore, SOAEs are dependent on the presence of a dip and not vice versa [18].
Frequency/Threshold Response at the Dip: The frequency threshold curves of single ANFs, expressed as Q10dB, were found to range from 1 to 4 for fibers with CFs below 2 kHz and from 3 to 15 with CFs near 10 kHz [19].
The dip in the HT around the HF (Figure 1) resembles the frequency threshold curves of spike discharges in isolated single ANFs. The sharpness of the dip on average 15 in Table 3, expressed as Q10dB, is abnormally high compared to the frequency threshold curves of single ANFs.
The presence of a dip in the HT around the HF in the right ear enables the hum to interact with adjacent ESs in perceivable interactions of periodic pulling and synchronization. When hum was present, the dip also was present but masked by the nonlinear behavior of hum. About 2 Hz away from the HF, the HTs were significantly lower when hum was present than during an absent hum, indicating a 5-10 dB better HT in the presence of hum. When hum was absent for a short duration after air travel, jogging or ASA consumption, the dip did not seem to change shape but shifted into worse HTs (Figure 2).
Mechano-to-Electrical and Electro-to-Mechanical Conversions: The VHCs and basal OHCs respond to sound stimuli by generating VMs and CMs that superimpose synchronously in-phase. VMs and CMs oscillate in-phase with the displacement of the cupula (or tectorial membrane) [14].
It has long been known, but hardly believed, that VHCs can convert acoustic signals into VMs up to the ultrasonic range [20].
The electromotility of OHCs causes voltage-induced length variations of up to 32 kHz. A distinctive feature of OHC electromotility is that it follows changes in membrane potentials and not ionic currents and that frequency tuning is absent in voltage-driven length oscillations of single OHCs from all turns [21].
The latencies of the mechano-to-electrical transducer channels of the VHCs and the electro-to-mechanical transducer processes of the OHCs are below 100 μs and may act similar to piezoelectricity [22].
Proposed Area of Energy Conversions: The VCIA can be described as the area where mechanical energy is converted to electrical energy in the vestibule, which is subsequently converted back to mechanical energy by the OHCs in the cochlear base.
Through sound exposure, in the first step, VHCs may take over the conversion of sound pressure waves into VMs, which excite the bulk of parallel acting OHCs of the cochlear base to synchronous mechanical longitudinal oscillation. This generates sound pressure waves that feedback to a bulk of parallel acting VHCs and stimulate them to form additional VMs, which in turn again excite OHCs, thus tuning and completing a synchronous mechanical to electrical plus electrical to mechanical slightly damped circuit.
As long as these conversions run as subthreshold background oscillations, they may run just at the border of a self-sustained oscillation without CMs being formed by the OHCs.
Furthermore, when the signal strength is above HT, presumably initiated by an intense hum or an ES, a motion-induced shear force is generated at OHCs in the VCIA. The signal strength is then above HT and may generate receptor currents, known as CMs, by rhythmically opening and closing the transduction channels of the stereocilia that are in resonance with the subthreshold mechanical background oscillation and amplifying them. The vibration activates the neighboring IHCs and their afferent neurons in the VCIA, resulting in two effects: the information is sent in-phase without time delay [9] throughout the cochlea as CM along Nuel’s tunnel, and afferent neurons send the information to the brain, where it is converted into an efferent feedback signal that is sent to the OHCs of the excited ear.
Mechano-to-Electrical to Mechanical Conversions in Hum-Oscillations: Afferent and efferent innervations were found in all VHCs in the semicircular canals, consisting of two types of VHCs with resting discharge rates varying from a few to over 200 spikes/s. Type II VHCs fire more regularly because their activity is received from several VHCs of this type in a tonic response form [15].
Concerning cochlear hair cells, it is well known that the vast majority of afferent innervations originate from IHCs, and each afferent neuron supplies only one IHC, whereas the vast majority of efferent innervations terminate at OHCs, and each efferent neuron supplies several OHCs.
At rest, the activation of hum-oscillations between mechanical to electrical and electrical to mechanical energies can be assumed to be initiated by resonance oscillation of the system in the VCIA and, in the absence of other identifiable alternatives, to be transported via extensive vestibular afferent innervations to the brain. This may be why the subjects hum is perceived in the left upper head region at rest. When an ES is delivered to the right ear, the position of the hum impression shifts immediately to the right ear, resulting in the typical interactions between hum and ESs in the right ear [3].
If we assume that there is no voltage-controlled frequency tuning of the length oscillations of individual OHCs, the CF cannot be activated by the CM along the Nuel tunnel alone. Additional efferent feedback could cause a frequency-sharpening interaction, which could be in parallel to the interaction with the traveling wave.
Conclusion
The vestibule and cochlea base seem to play a crucial role in the generation/elimination of hum and of an accompanying dip.
The most likely location of the hum appears to be an area spanning the vestibule and cochlear base, which we refer to as the Vestibular–Cochlea Interaction Area (VCIA). In the VCIA, the conversion of mechanical energy to electrical energy appears to occur in the vestibule, and subsequent conversion of this electrical energy to mechanical energy occurs at the OHCs in the cochlear base. These ongoing conversions appear to occur in a coordinated fashion, resulting in the generation of a damped synchronous oscillation that likely tune and amplifies the hum and appear to be the starting point for sound processing.
A dip seems to be located in the area around the CF in the cochlea generated by the same mechanism, which is also responsible for generating the critical bands and sound interacting properties of the hum.
Studies on the behaviors of interactive hum seem to provide interesting clues to where and how hum arises and insights into previously unexplained phenomena in the hearing process.
References
- Mullins JH, Kelly JP. The mystery of the Taos hum. Echoes. 1995;5(3):1-6.
- Frosch FG. Possible Joint Involvement of the Cochlea and Semicircular Canals in the Perception of Low-Frequency Tinnitus, Also Called "The Hum" or "Taos Hum". The Int Tinnitus J. 2017;21(1):63-7.
- Frosch FG. Hum and otoacoustic emissions may arise out of the same mechanisms. J Sci Explor. 2013;27(4):603-24.
- Frosch FG. Manifestations of a low-frequency sound of unknown origin perceived worldwide, also known as "the Hum" or the "Taos Hum". The Int Tinnitus J. 2016;20(1):59-63.
- Frosch FG. Possible joint involvement of the cochlea and semicircular canals in the perception of low-frequency tinnitus, also called “the Hum” or “Taos hum”. Int Tinnitus J. 2017;21(1):63-67.
- Wever EG. Beats and related phenomena resulting from the simultaneous sounding of two tones: Psychol Rev. 1929;36(5): 402-523.
- Kellaway P. The mechanism of the electrophonic effect. J Neurophysiol. 1946;9(1):23-31.
- Schreiner CE, Langner G. Laminar fine structure of frequency organization in auditory midbrain. Nature. 1997;388(6640):383-6.
- Tasaki I, Davis H, Legouix JP. The space-time pattern of the cochlear microphonics (guinea pig), as recorded by differential electrodes. JASA 1952;24(5):502-19.
- He W, Porsov E, Kemp D, Nuttall AL, Ren T. The group delay and suppression pattern of the cochlear microphonic potential recorded at the round window. PLoS One. 2012;7(3)e34356:1-9.
- Oxenham AJ. How we hear: The perception and neural coding of sound. Annu Rev of psychol. 2018;69:27-50.
- Braun M. Dual Tuning In The Mammalian Cochlea: Dissociation Of Neural And Basilar Membrane Responses At Supra-Threshold Sound Levels–A Meta-Analysis. Inconcepts and Challenges in the Biophysics of Hearing: (With CD-ROM). 2009:162-7.
- McCue MP, Guinan Jr JJ. Sound-evoked activity in primary afferent neurons of a mammalian vestibular system. The Am J Otol. 1997;18(3):355-60.
- De Vries H, Vrolijk JM. Phase relations between the microphonic crista effect of the three semi-circular canals, the cochlear microphonics and the motion of the stapes. Acta oto-laryngologica. 1953;43(1):80-9.
- Goldberg JM, Fernandez C. Physiology of peripheral neurons innervating semicircular canals of the squirrel monkey. I. Resting discharge and response to constant angular accelerations. J Neurophysiol. 1971;34(4):635-60.
- Wilson JP. Evidence for a cochlear origin for acoustic re-emissions, threshold fine-structure and tonal tinnitus. Hear Res. 1980;2:233-52.
- Sachs MB, Young ED. Encoding of steady-state vowels in the auditory nerve: representation in terms of discharge rate. The J the Acoustica Soc Am. 1979;66(2):470-9.
- Schloth E. Relation between spectral composition of spontaneous oto-acoustic emissions and fine-structure of threshold in quiet. Acta Acustica United with Acustica. 1983;53(5):250-6.
- Evans E. The frequency response and other properties of single fibres in the guinea-pig cochlear nerve. The J physiol. 1972;226(1):263-87.
- Trincker D, Partsch CJ. The AC Potentials (Microphonics) from the Vestibular Apparatus. Ann of Otol, Rhinol & Laryngol. 1959;68(1):153-8.
- Gitter AH, Zenner HP. Electromotile responses and frequency tuning of isolated outer hair cells of the guinea pig cochlea. Eur Arch of Oto-Rhino-laryngol. 1995;252(1):15-9.
- Brown DJ, Pastras CJ, Curthoys IS. Electrophysiological measurements of peripheral vestibular function—A review of electrovestibulography. Front in SystsNeurosci. 2017;11:34.
Private Initiative Brummton, Bad Dürkheim, Germany
Send correspondence to:
Dr. Franz Günter Frosch
Private Initiative Brummton, Auf dem Köppel 1 Nr. 11, D-67098, Bad Dürkheim, Germany. E-mail: Frosch.com@t-online.de.
Paper submitted on March 07, 2022; and Accepted on April 04, 2022
Citation: Franz Günter Frosch. A Resonant Circuit Involving the Vestibule and Cochlea Base Could Cause Extremely Low-Frequency Tinnitus, also Called “The Hum” or “Taos Hum”. Int Tinnitus J. 2022;26(1):42-49.